Choose your Gem:
One of a kind. 108 Million Pixels.
OpenSea NFT opens in a new tab. Connect wallet to buy!
Current Pricing
NFT value changes over time. Rarity and value increases as the set availability decreases.
1.0000♦ ETH
Approximate Exchange Rates:◦ BTC: 0.056287
◦ EUR: 1096.541076
◦ USD: 1133.619449
Width (px)
Height (px)
Total Pixels
Remaining Available
Current Decrypted Data:
Mathematics & Geometry
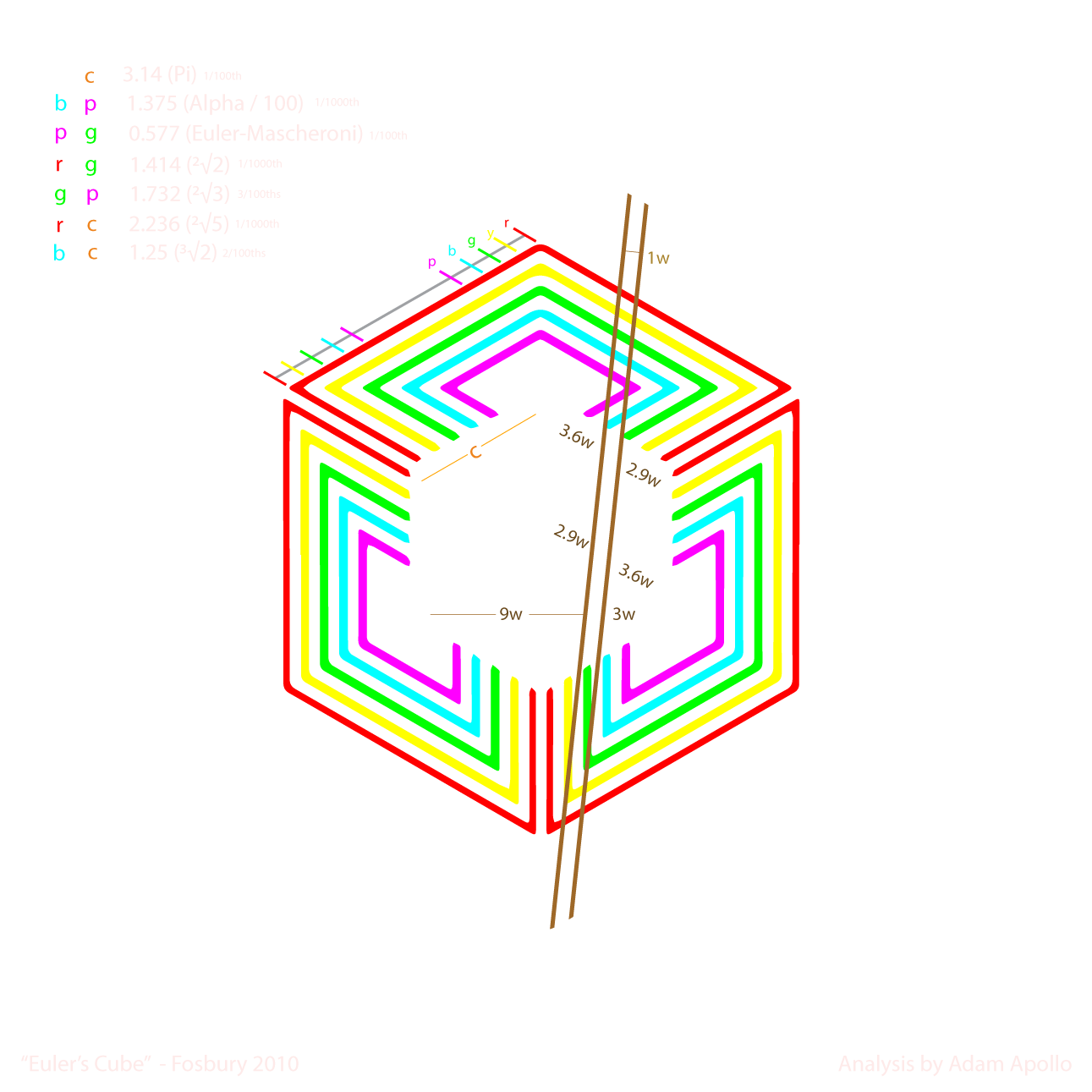
Analysis of the crop circle which appeared in Fosbury Wiltshire UK on July 17th 2010 reveals a sequence of mathematical constants embedded in the proportions of the harmonic sequence of hypercubes within the structure. These constants include (with accuracy):
3.14 Pi = Outer Hexagon Edge / Inner Cube Edge (1/100th)
1.375 Alpha x 100 = Blue Edge / Pink Edge (1/1000th)
0.577 Euler-Mascheroni = Pink Edge / Green Edge (1/100th)
1.414 Square Root of 2 = Red Edge / Green Edge (1/1000th)
1.732 Square Root of 3 = Green Edge / Pink Edge (3/100ths)
2.236 Square Root of 5 = Red Edge / Inner Cube Edge (1/1000th)
1.25 Cube Root of 2 = Blue Edge / Inner Cube Edge (2/100ths)
Note the diagram below for measurements and color coding.
It is also notable that the positioning of this crop circle is perfectly oriented relative to the tire tracks running through the inner cube, such that there is a perfect proportional balance between where the tracks enter and exit the cube sides.

Analysis by Carissa Ouellette

Analysis by Carissa Ouellette
Euler's Constant Analysis
On July 17th 2010 near Vernham Dean, Wiltshire, UK the 250ft Fosbury crop circle was sighted. While many have looked at this crop through a 3 dimensional perspective linking its geometry to the Tesseract (or Hypercube), an even more intriguing perspective is hidden within a 2 dimensional analysis of the crop.
You can look at the crop as if it were a smaller cube nested inside a larger cube with some interesting nested divisions of the faces of the external cube’s faces. This is where some of the hypercube interpretations begin and end, really. However, if you take to analyzing the projections of the cubes onto the 2D plane, you begin to see nested hexagons.
After Adam Apollo performed his analysis on the hexagon (or cube) edge lengths, an interesting connection between the inner hexagon and outer hexagon edge lengths emerged. While the outer hexagon edge length to the edge length of the flattened crop gave Pi, the same outer hexagon edge length to the full “hidden” inner cube (including its border) gives Euler’s number!
EdgeLengthOUTER / EdgeLengthINNER ≈ e = Euler’s Constant
2.71318 ≈ 2.71828
Now, if you were to nest a circle inside the perimeter of each of the INNER and OUTER 2D hexagons, this would be the same as nesting two spheres inside each cube. Where,
EdgeLengthOUTER = SphereDiameterOUTER, and
EdgeLengthINNER = SphereDiameterINNER
Bringing this back into the 2D space, we know the diameter of a sphere is equal to the diameter of its 2D projection of a circle so we can also say,
DOUTER / DINNER = e
Now that we can see the Euler relationship down in the 2D plane with circles representing spheres, we continue to nest circles inside the perimeter of the each of the remaining 5 hexagons present between the inner and outer hexagons. We find that each of the 5 circles have diameters that divide the space between the inner and outer circles by equal 12ths. If you were to fully divide the space by circles, their diameters would be
DN = DINNER + N*(DOUTER – DINNER) / 12
Where N = 1,..,12
From here we can begin to see a relationship emerge: a division of space in 12ths with a growth (or decay) rate of e.
Music theory and the Circle of 5ths is a great analogous tool to describe this infinite division of space. If we map the 12 axial divisions of the Circle of 5ths onto our circular map, we can more easily imagine the traversal of the 12 Major notes in the Circle of 5ths (C, G, D, A , E, B, F#, Db, Ab, Eb, Bb, F) as if each note were mapped to each circle (or sphere). Now, we know that we can continuously traverse the Circle of 5ths into ever growing, or decaying harmonic frequencies within audible range. We can visualize this traversal through the use of an Archimedes spiral connecting the edge of each successive circle to the 12 major axial divisions of the space. (See image below.)
We can further the visual exercise by repeating the pattern in either a growth or decay representation by repeating the pattern with another set of circles with each of their diameters scaled by a factor e. Outside the bounds of the analogy of audible frequencies, we can extrapolate a relationship between spheres, their diameters, and potentially their resonant frequencies.
We know that where Euler’s constant shows up, there is usually a natural growth or decay function being described that can often be measured in nature. Can this relationship credit Pythagoras for the discovery of music theory’s harmonious Circle of 5ths being yet another description of a natural growth and decay phenomena? Or perhaps this interesting relationship is one we can use to describe other physical phenomena in our 3D reality. It’s open to further investigation.
– Analysis by Carissa Ouellette


Don’t miss the next releases…
These Galactic NFTs are going quickly, so jump on our list to find out when the next release is coming, so you can be ready!
We believe in personal data sovereignty. We will never sell your information to third parties. We will always protect your email address. We will never spam you. We will always respect your requests.